Qu’est-ce que
la parallaxe solaire ?
D’une façon générale, la parallaxe peut être définie
comme la différence entre les directions d’un corps
observé depuis deux points de vue différents.
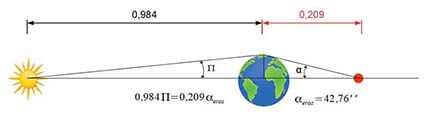
La parallaxe solaire est la parallaxe horizontale du Soleil. C’est un petit angle d’un grand triangle rectangle céleste ayant le rayon de la Terre comme côté opposé et la distance entre les centres de la Terre et du Soleil comme hypoténuse. La connaissance de cet angle fixe donc la distance au Soleil – pourvu que l’on connaisse le rayon terrestre. Cette distance est baptisée unité astronomique et représentée par le seul symbole au.
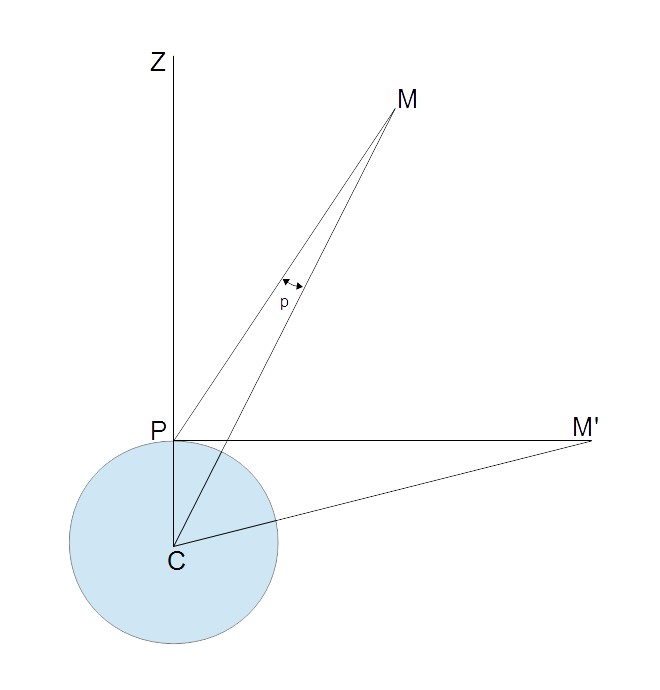
figure 1 – la parallaxe solaire.
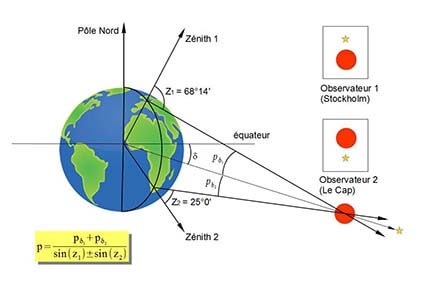
La parallaxe p d’un corps céleste est la différence entre la direction d’un corps céleste M vu depuis le centre de la Terre C et celle où il est vu par un observateur P situé à la surface de la Terre. Si le corps se trouve au zénith Z du lieu, la parallaxe sera nulle. S’il se trouve à l’horizon au point M’, sa parallaxe sera maximale et prendra la dénomination de parallaxe horizontale. Crédits P. Descamps
Toutefois, pour être complètement rigoureux, la parallaxe solaire n’est que la forme abrégée de la parallaxe horizontale équatoriale du Soleil. Compte-tenu de la forme aplatie aux pôles de la Terre, c’est le rayon équatorial qui intervient dans la définition de la parallaxe solaire (figure 2).
De plus, la distance de la Terre au Soleil varie constamment, de sorte que c’est sa valeur moyenne qui est prise en considération. Il en va bien évidemment de même pour tout autre corps céleste, planètes ou étoiles.
Ainsi, quand nous disons que la parallaxe horizontale de la Lune est de 57ʹ, cela revient à dire que le diamètre de la Terre vu depuis le centre de la Lune présente une taille angulaire apparente égale à deux fois cette valeur, soit 1,9°.
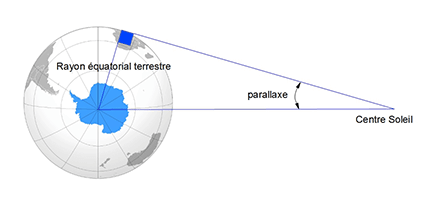
figure 2 – définition de la parallaxe horizontale équatoriale du Soleil, plus simplement appelée « parallaxe solaire ».
Crédits P. Descamps
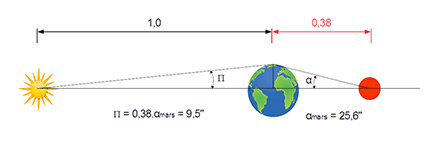
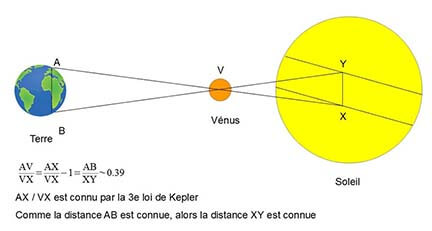
Nous connaissons également les distances des différentes planètes au Soleil sous la forme de proportions entre elles qui n’ont que peu changé depuis les temps historiques de Copernic et Kepler, de sorte que la mesure d’une seule de ces distances donne immédiatement la connaissance de toutes les autres, et, par conséquent, la taille du Système solaire.
C’est pourquoi la détermination de la parallaxe solaire peut être obtenue à partir de la mesure de la parallaxe de n’importe quel corps du Système solaire, dès lors que l’on connaît le rapport des distances relatives à la Terre du corps considéré et du Soleil.